Predict House price

10 minute read

Objective: To determine the price of the house using deep neural network. We’ve been provided with historical data and fetaures of the house.

Source: Udemy | Python for Data Science and Machine Learning Bootcamp
Data used in the below analysis: Housing data from Kaggle.

#Importing libraries as required
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

%matplotlib inline

sns.set_style('whitegrid')

data = pd.read_csv('DATA/kc_house_data.csv') #read dataset

Starting with some EDA! (Explanatory Data Analysis)

data.isnull().sum() #checking for null data

id               0
date             0
price            0
bedrooms         0
bathrooms        0
sqft_living      0
sqft_lot         0
floors           0
waterfront       0
view             0
condition        0
grade            0
sqft_above       0
sqft_basement    0
yr_built         0
yr_renovated     0
zipcode          0
lat              0
long             0
sqft_living15    0
sqft_lot15       0
dtype: int64

The data has no null values

#viewing some basic info about the dataset
data.describe().transpose()

	count	mean	std	min	25%	50%	75%	max
id	21597.0	4.580474e+09	2.876736e+09	1.000102e+06	2.123049e+09	3.904930e+09	7.308900e+09	9.900000e+09
price	21597.0	5.402966e+05	3.673681e+05	7.800000e+04	3.220000e+05	4.500000e+05	6.450000e+05	7.700000e+06
bedrooms	21597.0	3.373200e+00	9.262989e-01	1.000000e+00	3.000000e+00	3.000000e+00	4.000000e+00	3.300000e+01
bathrooms	21597.0	2.115826e+00	7.689843e-01	5.000000e-01	1.750000e+00	2.250000e+00	2.500000e+00	8.000000e+00
sqft_living	21597.0	2.080322e+03	9.181061e+02	3.700000e+02	1.430000e+03	1.910000e+03	2.550000e+03	1.354000e+04
sqft_lot	21597.0	1.509941e+04	4.141264e+04	5.200000e+02	5.040000e+03	7.618000e+03	1.068500e+04	1.651359e+06
floors	21597.0	1.494096e+00	5.396828e-01	1.000000e+00	1.000000e+00	1.500000e+00	2.000000e+00	3.500000e+00
waterfront	21597.0	7.547345e-03	8.654900e-02	0.000000e+00	0.000000e+00	0.000000e+00	0.000000e+00	1.000000e+00
view	21597.0	2.342918e-01	7.663898e-01	0.000000e+00	0.000000e+00	0.000000e+00	0.000000e+00	4.000000e+00
condition	21597.0	3.409825e+00	6.505456e-01	1.000000e+00	3.000000e+00	3.000000e+00	4.000000e+00	5.000000e+00
grade	21597.0	7.657915e+00	1.173200e+00	3.000000e+00	7.000000e+00	7.000000e+00	8.000000e+00	1.300000e+01
sqft_above	21597.0	1.788597e+03	8.277598e+02	3.700000e+02	1.190000e+03	1.560000e+03	2.210000e+03	9.410000e+03
sqft_basement	21597.0	2.917250e+02	4.426678e+02	0.000000e+00	0.000000e+00	0.000000e+00	5.600000e+02	4.820000e+03
yr_built	21597.0	1.971000e+03	2.937523e+01	1.900000e+03	1.951000e+03	1.975000e+03	1.997000e+03	2.015000e+03
yr_renovated	21597.0	8.446479e+01	4.018214e+02	0.000000e+00	0.000000e+00	0.000000e+00	0.000000e+00	2.015000e+03
zipcode	21597.0	9.807795e+04	5.351307e+01	9.800100e+04	9.803300e+04	9.806500e+04	9.811800e+04	9.819900e+04
lat	21597.0	4.756009e+01	1.385518e-01	4.715590e+01	4.747110e+01	4.757180e+01	4.767800e+01	4.777760e+01
long	21597.0	-1.222140e+02	1.407235e-01	-1.225190e+02	-1.223280e+02	-1.222310e+02	-1.221250e+02	-1.213150e+02
sqft_living15	21597.0	1.986620e+03	6.852305e+02	3.990000e+02	1.490000e+03	1.840000e+03	2.360000e+03	6.210000e+03
sqft_lot15	21597.0	1.275828e+04	2.727444e+04	6.510000e+02	5.100000e+03	7.620000e+03	1.008300e+04	8.712000e+05

data.head()

	id	date	price	bedrooms	bathrooms	sqft_living	sqft_lot	floors	...	grade	sqft_above	sqft_basement	yr_built	yr_renovated	zipcode	lat	long	sqft_living15	sqft_lot15
0	7129300520	10/13/2014	221900.0	3	1.00	1180	5650	1.0	...	7	1180	0	1955	0	98178	47.5112	-122.257	1340	5650
1	6414100192	12/9/2014	538000.0	3	2.25	2570	7242	2.0	...	7	2170	400	1951	1991	98125	47.7210	-122.319	1690	7639
2	5631500400	2/25/2015	180000.0	2	1.00	770	10000	1.0	...	6	770	0	1933	0	98028	47.7379	-122.233	2720	8062
3	2487200875	12/9/2014	604000.0	4	3.00	1960	5000	1.0	...	7	1050	910	1965	0	98136	47.5208	-122.393	1360	5000
4	1954400510	2/18/2015	510000.0	3	2.00	1680	8080	1.0	...	8	1680	0	1987	0	98074	47.6168	-122.045	1800	7503

5 rows × 21 columns

#looking at the price range, the feature to be predicted
plt.figure(figsize=(12,8))
sns.distplot(data['price'])

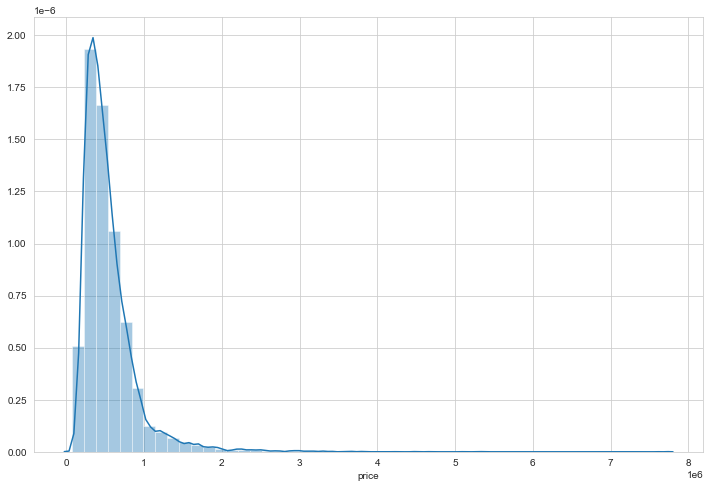
The data is mostly concentrated around 1,000,000 - 2,000,000 with few houses at 3,000,000 and even at around 7,500,000

sns.countplot(data['bedrooms'])

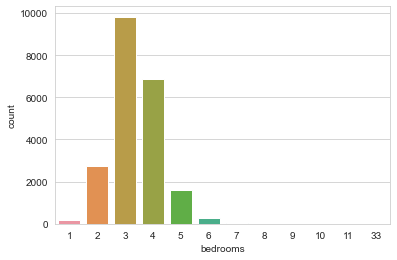
The data mostly contains houses with 3 bedrooms

#Checking the correlation of price with other features!
data.corr()['price'].sort_values()

zipcode         -0.053402
id              -0.016772
long             0.022036
condition        0.036056
yr_built         0.053953
sqft_lot15       0.082845
sqft_lot         0.089876
yr_renovated     0.126424
floors           0.256804
waterfront       0.266398
lat              0.306692
bedrooms         0.308787
sqft_basement    0.323799
view             0.397370
bathrooms        0.525906
sqft_living15    0.585241
sqft_above       0.605368
grade            0.667951
sqft_living      0.701917
price            1.000000
Name: price, dtype: float64

The most correlated is the Square footage of the apartments interior living space with 0.71. We can see that in the below plot as well!

plt.figure(figsize=(12,8))
sns.scatterplot(x='price',y='sqft_living',data=data)

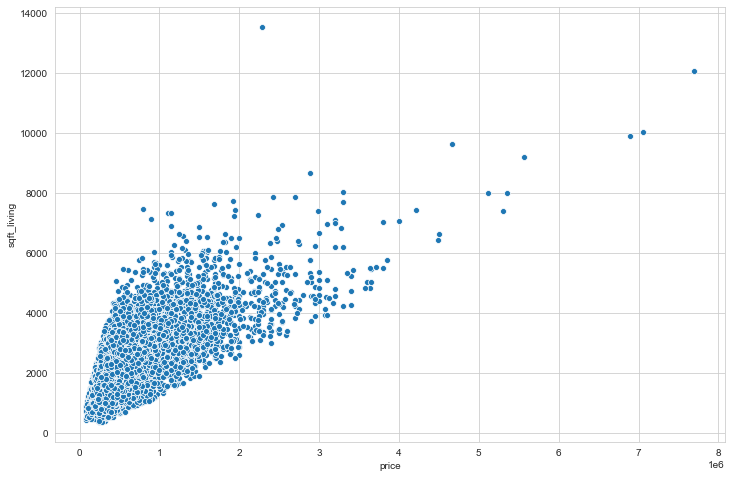
#Num of bedrooms vs price of the house
plt.figure(figsize=(15,10))
sns.boxplot(x='bedrooms',y='price',data=data)

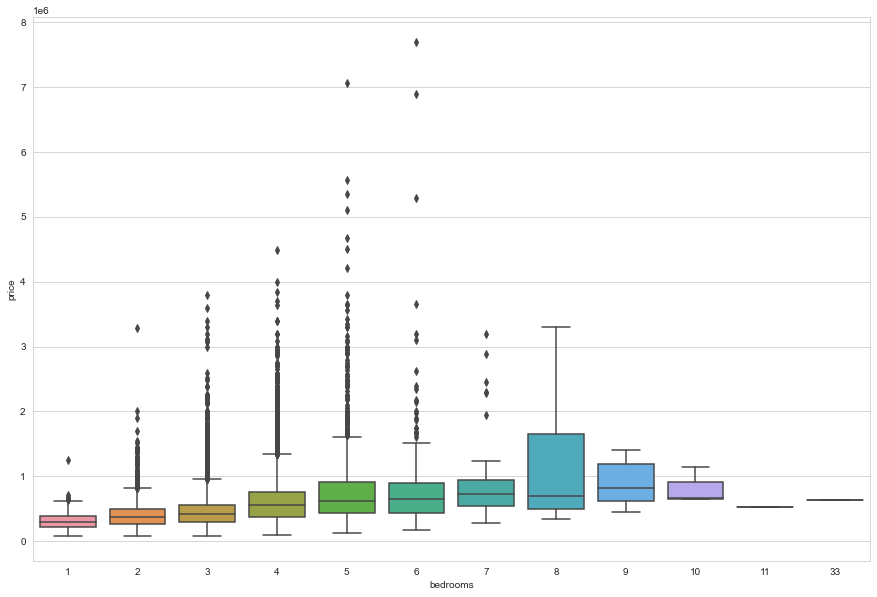
#price vs longitude
plt.figure(figsize=(12,8))
sns.scatterplot(x='price',y='long',data=data)

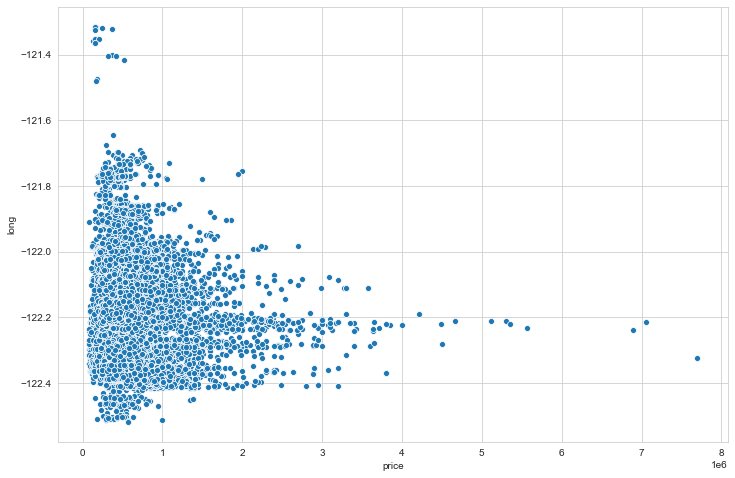
#price vs latitude
plt.figure(figsize=(12,8))
sns.scatterplot(x='price',y='lat',data=data)

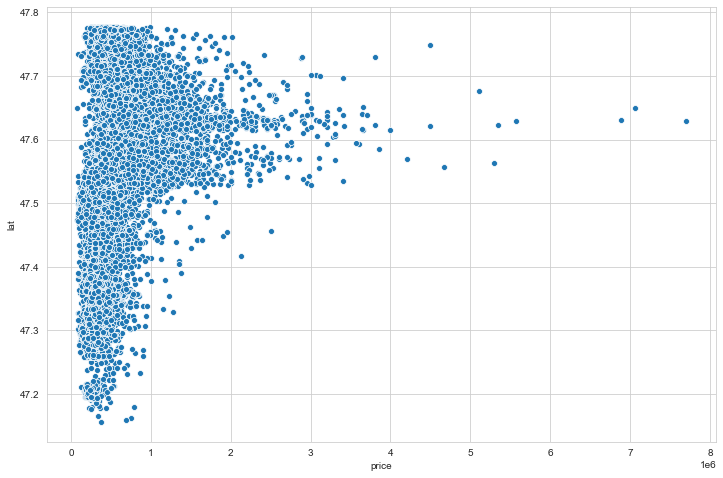
#plotting price with longitude and langitude can give us expensive areas in the given region
plt.figure(figsize=(12,8))
sns.scatterplot(x='long',y='lat',data=data,hue='price')

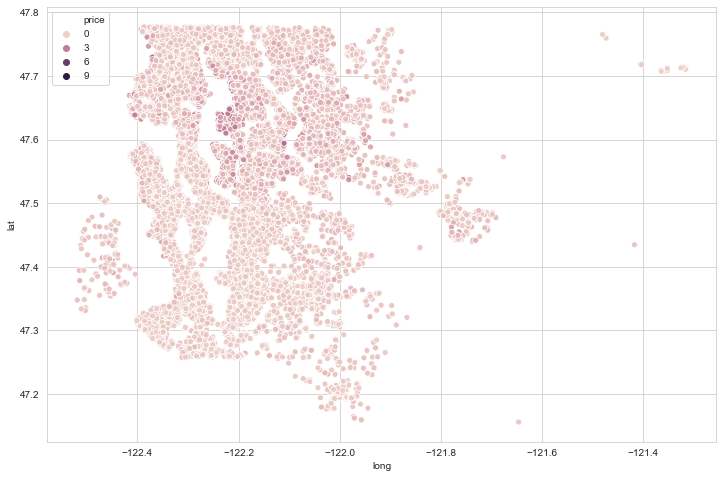
We can clean data to get a better plot of house prices

#getting the price outliers - most priced houses
data.sort_values('price',ascending=False).head(20)

	id	date	price	bedrooms	bathrooms	sqft_living	sqft_lot	floors	waterfront	view	...	grade	sqft_above	sqft_basement	yr_built	yr_renovated	zipcode	lat	long	sqft_living15	sqft_lot15
7245	6762700020	10/13/2014	7700000.0	6	8.00	12050	27600	2.5	0	3	...	13	8570	3480	1910	1987	98102	47.6298	-122.323	3940	8800
3910	9808700762	6/11/2014	7060000.0	5	4.50	10040	37325	2.0	1	2	...	11	7680	2360	1940	2001	98004	47.6500	-122.214	3930	25449
9245	9208900037	9/19/2014	6890000.0	6	7.75	9890	31374	2.0	0	4	...	13	8860	1030	2001	0	98039	47.6305	-122.240	4540	42730
4407	2470100110	8/4/2014	5570000.0	5	5.75	9200	35069	2.0	0	0	...	13	6200	3000	2001	0	98039	47.6289	-122.233	3560	24345
1446	8907500070	4/13/2015	5350000.0	5	5.00	8000	23985	2.0	0	4	...	12	6720	1280	2009	0	98004	47.6232	-122.220	4600	21750
1313	7558700030	4/13/2015	5300000.0	6	6.00	7390	24829	2.0	1	4	...	12	5000	2390	1991	0	98040	47.5631	-122.210	4320	24619
1162	1247600105	10/20/2014	5110000.0	5	5.25	8010	45517	2.0	1	4	...	12	5990	2020	1999	0	98033	47.6767	-122.211	3430	26788
8085	1924059029	6/17/2014	4670000.0	5	6.75	9640	13068	1.0	1	4	...	12	4820	4820	1983	2009	98040	47.5570	-122.210	3270	10454
2624	7738500731	8/15/2014	4500000.0	5	5.50	6640	40014	2.0	1	4	...	12	6350	290	2004	0	98155	47.7493	-122.280	3030	23408
8629	3835500195	6/18/2014	4490000.0	4	3.00	6430	27517	2.0	0	0	...	12	6430	0	2001	0	98004	47.6208	-122.219	3720	14592
12358	6065300370	5/6/2015	4210000.0	5	6.00	7440	21540	2.0	0	0	...	12	5550	1890	2003	0	98006	47.5692	-122.189	4740	19329
4145	6447300265	10/14/2014	4000000.0	4	5.50	7080	16573	2.0	0	0	...	12	5760	1320	2008	0	98039	47.6151	-122.224	3140	15996
2083	8106100105	11/14/2014	3850000.0	4	4.25	5770	21300	2.0	1	4	...	11	5770	0	1980	0	98040	47.5850	-122.222	4620	22748
7028	853200010	7/1/2014	3800000.0	5	5.50	7050	42840	1.0	0	2	...	13	4320	2730	1978	0	98004	47.6229	-122.220	5070	20570
19002	2303900100	9/11/2014	3800000.0	3	4.25	5510	35000	2.0	0	4	...	13	4910	600	1997	0	98177	47.7296	-122.370	3430	45302
16288	7397300170	5/30/2014	3710000.0	4	3.50	5550	28078	2.0	0	2	...	12	3350	2200	2000	0	98039	47.6395	-122.234	2980	19602
18467	4389201095	5/11/2015	3650000.0	5	3.75	5020	8694	2.0	0	1	...	12	3970	1050	2007	0	98004	47.6146	-122.213	4190	11275
6502	4217402115	4/21/2015	3650000.0	6	4.75	5480	19401	1.5	1	4	...	11	3910	1570	1936	0	98105	47.6515	-122.277	3510	15810
15241	2425049063	9/11/2014	3640000.0	4	3.25	4830	22257	2.0	1	4	...	11	4830	0	1990	0	98039	47.6409	-122.241	3820	25582
19133	3625049042	10/11/2014	3640000.0	5	6.00	5490	19897	2.0	0	0	...	12	5490	0	2005	0	98039	47.6165	-122.236	2910	17600

20 rows × 21 columns

We can disregard a % of entries to remove outliers and get better model predictions!

len(data)*0.01

215.97

non_top_1_percent = data.sort_values('price',ascending=False).iloc[216:]

plt.figure(figsize=(12,8))
sns.scatterplot(x='long',y='lat',data=non_top_1_percent,
                edgecolor=None, alpha=0.2, palette = 'RdYlGn', hue='price')

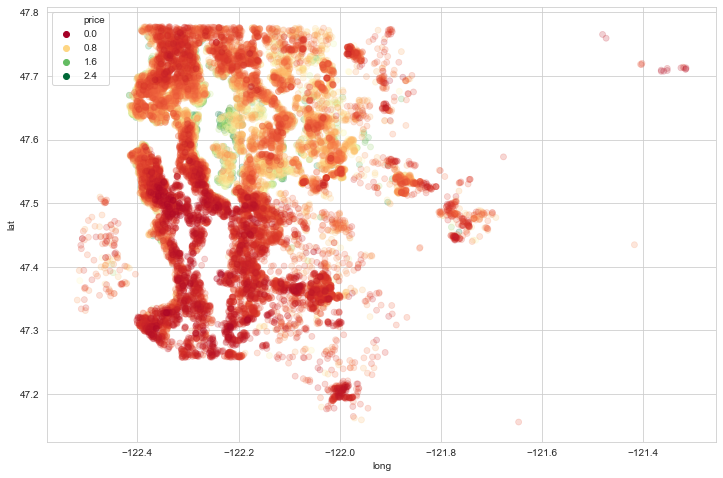
We can clearly see the most expensive housing areas now!

#Checking the price of houses on the waterfront
#As per the above plot, they seem to be more expensive
sns.boxplot(x='waterfront',y='price',data=data)

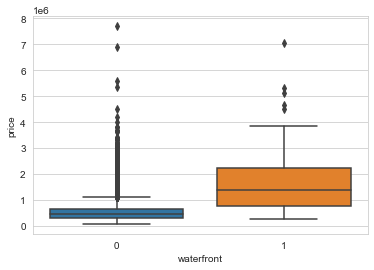
Start with feature engineering! We need to clean data for model to give better results!

#Dropping unnecessary fields!
data.drop('id',axis=1,inplace=True)

#converting date into something usefull
data['date'] = pd.to_datetime(data['date'])
data['year'] = data['date'].apply(lambda x : x.year)
data['month'] = data['date'].apply(lambda x : x.month)

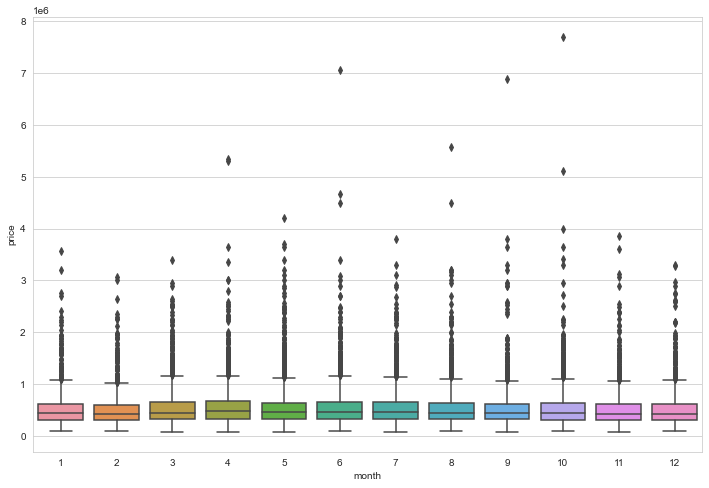
#checking month vs price of house
plt.figure(figsize=(12,8))
sns.boxplot(x='month',y='price',data=data)

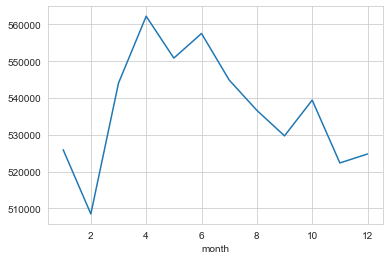
data.groupby(by='month').mean()['price'].plot()

#price vs year
data.groupby(by='year').mean()['price'].plot()

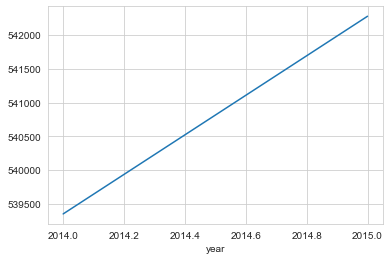
There seems to an expected relationship with year and mean prices of the house

data.drop('date',axis=1,inplace=True) #dropping date as we already have extracted its features

data['zipcode'].value_counts() #checking unique values to get the idea of the data

  602
  589
  583
  574
  553
        ...
  104
  100
   80
   57
   50
Name: zipcode, Length: 70, dtype: int64

#dropping as it don't seem to affect price much
#Seen before, has -ve correlation
data.drop('zipcode',axis=1,inplace=True)

data['yr_renovated'].value_counts()

     20683
     91
     37
     36
     35
        ...  
      1
      1
      1
      1
      1
Name: yr_renovated, Length: 70, dtype: int64

We can convert the above data into two options, renovated or non renovated for our price predictions. We are lucky we have years and renovated already in high correlation with price, intuitively we can use the data as is

data['sqft_basement'].value_counts()

     13110
     221
     218
     214
     206
        ...  
       1
      1
       1
      1
       1
Name: sqft_basement, Length: 306, dtype: int64

Same case with the basement area!

Training the model

#train test split
X = data.drop('price', axis=1).values
y = data['price'].values

from sklearn.model_selection import train_test_split
Xtrain, Xtest, ytrain, ytest = train_test_split(X,y,test_size = 0.3,
                                                random_state=101)

#Scaling the data
from sklearn.preprocessing import MinMaxScaler
scale = MinMaxScaler()
#fit and transform together
Xtrain = scale.fit_transform(Xtrain)
#we don't fit test data so that no info leak is there while training data
Xtest = scale.transform(Xtest)

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam

Creating a Sequential model with activation function as rectified linear, and a dense network where every neuron is connected to every other neuron. Also, the loss function used is Mean Squared Error and Adam is used as a gradient descent optimizer.

model = Sequential()

model.add(Dense(19,activation='relu'))
model.add(Dense(19,activation='relu'))
model.add(Dense(19,activation='relu'))
model.add(Dense(19,activation='relu'))
model.add(Dense(1))

model.compile(optimizer='adam',loss='mse')

model.fit(x=Xtrain,y=ytrain,
          validation_data=(Xtest,ytest),
          batch_size = 128, epochs=400)

Epoch 1/400
119/119 [==============================] - 0s 3ms/step - loss: 430242594816.0000 - val_loss: 418922102784.0000
Epoch 2/400
119/119 [==============================] - 0s 2ms/step - loss: 428868403200.0000 - val_loss: 413837787136.0000
Epoch 3/400
119/119 [==============================] - 0s 2ms/step - loss: 407161012224.0000 - val_loss: 363431297024.0000
Epoch 4/400
119/119 [==============================] - 0s 2ms/step - loss: 303796158464.0000 - val_loss: 206461501440.0000
Epoch 5/400
119/119 [==============================] - 0s 2ms/step - loss: 143996928000.0000 - val_loss: 98603425792.0000
.
.
.
Epoch 400/400
119/119 [==============================] - 0s 2ms/step - loss: 29113778176.0000 - val_loss: 26656872448.0000

losses = pd.DataFrame(model.history.history)

losses.plot()

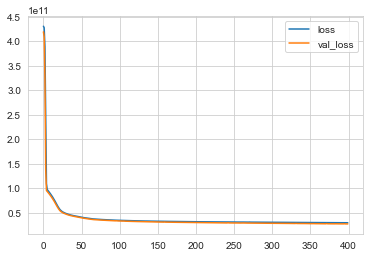
Expected behaviour of our model with loss vs Val_loss. We can train at more epochs as loss is still over val_loss and it’s not overfitting yet

Evaluating the model performance

from sklearn.metrics import mean_absolute_error, mean_squared_error, explained_variance_score

predictions = model.predict(Xtest)

print("Mean_absolute_error:", mean_absolute_error(ytest,predictions))
print("Mean_squared_error:",  mean_squared_error(ytest,predictions))
print("Root_Mean_Squared_error:", np.sqrt(mean_squared_error(ytest,predictions)))

Mean_absolute_error: 101612.238435571
Mean_squared_error: 26656866746.557117
Root_Mean_Squared_error: 163269.30742352377

data['price'].describe()['mean'] #checking the mean price

540296.5735055795

Our model is off by about 19% (Mean absolute error) of the mean value of price. It is not too bad but not great as such

#this tells how much variance our model can explain
#lower value is worse, best value is 1.0
explained_variance_score(ytest,predictions)

0.799128091503277

plt.figure(figsize=(12,6))
plt.scatter(ytest,predictions)
# Perfect predictions
plt.plot(ytest,ytest,'r')

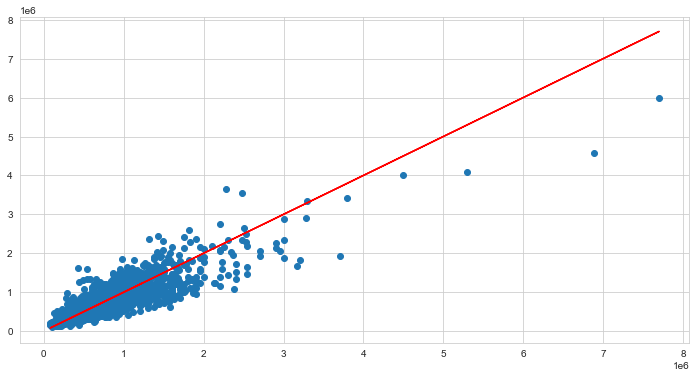
The plot of predicted vs true values seem fine except for some outliers

Predicting a new value

single_house = data.drop('price',axis=1).iloc[0] #creating a entry to check the model

single_house = scale.transform(single_house.values.reshape(-1, 19)) #transform to fit into model

print("Error:", abs(data.iloc[0]['price']-model.predict(single_house)[0][0]))

Error: 63496.40625

We can try to reduce error on the current rendered model by removing outliers and by increasing the epochs. We’ll try with removing outliers.

Re-training and evaluating the model

non_top_1_percent.drop('id',axis=1,inplace=True)
non_top_1_percent['date'] = pd.to_datetime(non_top_1_percent['date'])
non_top_1_percent['year'] = non_top_1_percent['date'].apply(lambda x : x.year)
non_top_1_percent['month'] = non_top_1_percent['date'].apply(lambda x : x.month)
non_top_1_percent.drop('date',axis=1,inplace=True)
non_top_1_percent.drop('zipcode',axis=1,inplace=True)

#train test split
X = non_top_1_percent.drop('price', axis=1).values
y = non_top_1_percent['price'].values
Xtrain, Xtest, ytrain, ytest = train_test_split(X,y,test_size = 0.3,
                                                random_state=101)
Xtrain = scale.fit_transform(Xtrain)
Xtest = scale.transform(Xtest)

model.fit(x=Xtrain,y=ytrain,
          validation_data=(Xtest,ytest),
          batch_size = 128, epochs=400)

Epoch 1/400
117/117 [==============================] - 0s 3ms/step - loss: 24656377856.0000 - val_loss: 22707032064.0000
Epoch 2/400
117/117 [==============================] - 0s 2ms/step - loss: 21469505536.0000 - val_loss: 21987682304.0000
Epoch 3/400
117/117 [==============================] - 0s 2ms/step - loss: 21053581312.0000 - val_loss: 21625681920.0000
Epoch 4/400
117/117 [==============================] - 0s 2ms/step - loss: 20826849280.0000 - val_loss: 21429176320.0000
Epoch 5/400
117/117 [==============================] - 0s 3ms/step - loss: 20693381120.0000 - val_loss: 21351958528.0000
.
.
.
Epoch 400/400
117/117 [==============================] - 0s 2ms/step - loss: 12499646464.0000 - val_loss: 13185313792.0000

losses = pd.DataFrame(model.history.history)
losses.plot()

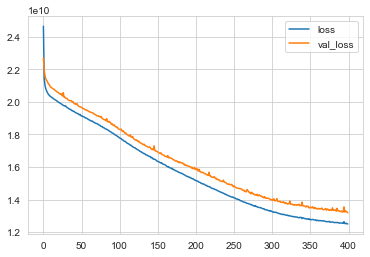
The new model shows some spikes in the val_loss which means its overfitting at 400 epochs. We’ll ignore them for now

predictions = model.predict(Xtest)

print("Mean_absolute_error:", mean_absolute_error(ytest,predictions))
print("Mean_squared_error:",  mean_squared_error(ytest,predictions))
print("Root_Mean_Squared_error:", np.sqrt(mean_squared_error(ytest,predictions)))
non_top_1_percent['price'].describe()['mean']

Mean_absolute_error: 75475.24519924006
Mean_squared_error: 13185316548.521532
Root_Mean_Squared_error: 114827.33362976575

518367.48037977645

explained_variance_score(ytest,predictions)

0.8400017690813121

plt.figure(figsize=(12,6))
plt.scatter(ytest,predictions)
# Perfect predictions
plt.plot(ytest,ytest,'r')

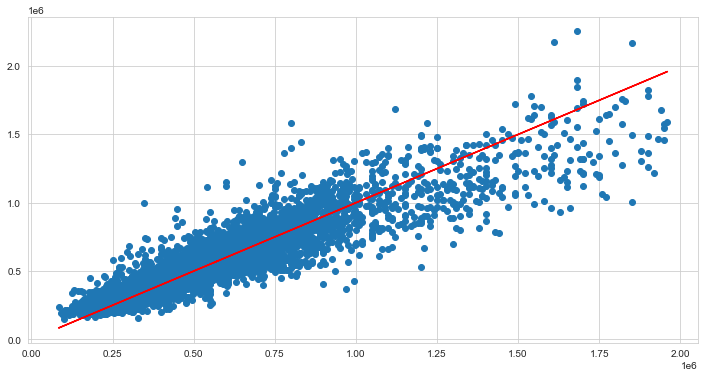
single_house = data.drop('price',axis=1).iloc[0]
single_house = scale.transform(single_house.values.reshape(-1, 19))

print("Error:", abs(data.iloc[0]['price']-model.predict(single_house)[0][0]))

Error: 39714.4375

The error in prediction has also reduced from before

Result: We were able to create a model and predict house prices post feature engineering and were also able to improve the error rate from 19% to 14.5%.

Our model is not great at predicting the outliers but can moslty predict values in the most common range.

The ability to explain variance has also increased from 80% to 84%.

Share on

Twitter Facebook Google+ LinkedIn

Vanya Sahu